A quick and easy solution using SQL and PL/SQL

What is the Traveling Salesman Problem?
Meet Tyrone. Tyrone works as a salesman for a young startup that sells energy-efficient air-conditioners. The head of Marketing and Sales was not happy with the results that the company's digital marketing campaigns have produced so far. She decides to allocate more resources in traditional marketing approaches such as roadshows. As part of this campaign, Tyrone was asked to visit the top 30 cities and towns (ranked by population), in his state. He was given a fixed budget to cover his expenses.
After reviewing the plan, Tyrone decided that instead of trying to make full use of the budget, he should find ways to cut down on unnecessary expenses as much as possible. The main expense that he had to plan for was accommodation and fuel. In order to save on fuel, he needs to spend as little time as possible on the road. In other words, he needs to plan a route that would cover all of the 30 stops and get him back home in the shortest possible distance.
This is a version of The Traveling Salesman problem. "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?". In this post, we explore a way to implement a solution using SQL and a little bit of PL/SQL.
STAGE 1: Data!
The dataset that we need to work on this problem is a set of addresses and the distances between each pair of addresses. I create a table to store this dataset.
create table distances
(origin varchar2(32767) --unique id for the address (Place ID)
,destination varchar2(32767) --unique id for the address (Place ID)
,distance number --distance from origin to destination
,origin_name varchar2(100)
,destination_name varchar2(100));I have a sample dataset that I have prepared using the Google Maps Platform. You could use this for the rest of the walkthrough. The sample dataset is a list of addresses of department stores and grocery stores in Alameda County in East Bay in California and the distances between each pair of addresses. In the walkthrough, we shall try to find the shortest route that connects all of these stores for a toilet paper purchase run that starts from Downtown Oakland.
Run the below script to load the dataset into the distances table.
STAGE 2: Permutations!
Now that we have a list of distances between each pair of addresses, the next task is to arrange them in sequences of addresses and then find the total distance covered in each sequence. One way to do this in Oracle would be to create a PL/SQL procedure that would sum up distances in a loop for each combination. While this approach would definitely give results, I took an alternate route. I used Hierarchical Queries in SQL. If you are completely new to Hierarchical Queries, I would recommend spending about 30 mins to go through explainers that are available online, before continuing with the rest of the walkthrough.
When you write a Hierarchical Query in SQL, a useful function that you get to use is the SYS_CONNECT_BY_PATH function. With this function, I can create a "path"/"route" in String format that goes through each of my addresses in a specific sequence. Let's go through the steps.
Step 1: a simple select * query to fetch all the rows in my distances table.
select *
from distances;
Step 2: converting this into a hierarchical query. Here, the destination address of one row will be the origin address in another row. For instance, if row 1 stores the distance from Walmart to Target, row 2 has the distance from Target to Home Depot and row 3 stores the distance from Home Depot to Whole Foods, then row 1 would be linked to row 2 since the destination in row 1 and the origin in row 2 are the same (Target). Similarly, row 2 would be linked to row 3, since the destination in row 2 is the same as the source in row 3 (Home Depot).
select *
from distances
connect by origin = prior destination;
Step 3: The data set contains information for combinations of addresses that would eventually result in loops. In the above example, if there is a row 4 that holds the distance from Whole Foods to Walmart, then we could end up with a CONNECT BY loop as we started from Walmart and the query could keep continuing along the same sequence of addresses. To handle this, we issue the NOCYCLE command to tell the SQL engine to stop processing the hierarchy when it encounters a loop and just return the row with the path constructed till then.
select *
from distances
connect by nocycle origin = prior destination;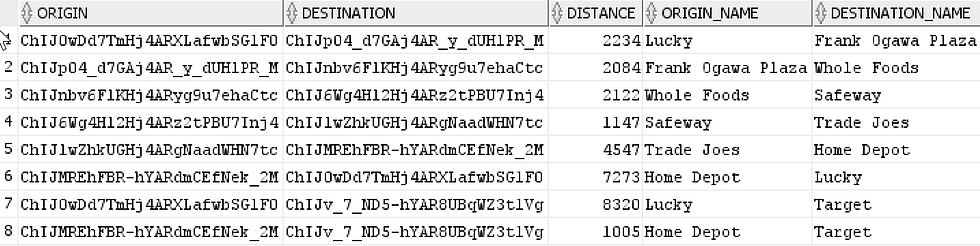
Step 4: now we introduce the SYS_CONNECT_BY_PATH function into the query to show us the path that each row has traversed.
select sys_connect_by_path(origin_name, ' - ') route
from distances
connect by nocycle origin = prior destination;
Step 5: let's clean up the path a bit by adding an LTRIM to take off the first delimiter
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ') route
from distances
connect by nocycle origin = prior destination;
Step 6: we will use the SYS_CONNECT_BY_PATH function on the distance column as well. Let's use the '+' sign as the delimiter here to signify that we are planning to add the distances.
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ') route
,ltrim(sys_connect_by_path(distance, '+'), '+') distance
from distances
connect by nocycle origin = prior destination;
Step 7: in the first row of output, the path shows the name of only one address. However, the row has a distance value next to it. This is the distance from the address in the origin column to the address in the destination column. In the first column, we are showing the path between all the origin addresses for all the rows that were fetched from the dataset when processing that path. The corresponding distances are shown in the second column. For the last origin address, the distance fetched is the distance between the address in the origin column and the address in the destination column. However, this address is not shown in the path in the first column. So, we'll concatenate the destination_name column to the route column in our query to make the path clear.
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,ltrim(sys_connect_by_path(distance, '+'), '+') distance
from distances
connect by nocycle origin = prior destination;
Step 8: let's now start filtering out unwanted rows. Since I have to visit all the addresses, I will filter out rows that are not going through all the addresses. In this walkthrough, I already know that the number of stops is 7. So I select only those rows which have 7 levels in their path.
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,ltrim(sys_connect_by_path(distance, '+'), '+') distance
from distances
where level = 7
connect by nocycle origin = prior destination;
Step 9: root of the route! Now we'll apply the TSP requirement which states that the route/path should start and finish at the same address. To do this, I make use of the CONNECT_BY_ROOT operator. This gives me the root address for each path. I just check if the destination of the row is the same as the root.
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,ltrim(sys_connect_by_path(distance, '+'), '+') distance
from distances
where level = 7
and connect_by_root origin = destination
connect by nocycle origin = prior destination;
You should now have 5040 paths to work with! Yay! Now, take a pencil and paper and start adding those distances. TSP solved! :)
STAGE 3: The hack!
If your basic math is as weak as mine, then summing up the distances using a pencil and paper is a no-go. Instead, I am calling in PL/SQL at this stage for some assist.
What we have now is a String that contains all the distances for each path. The task at hand is to sum these distances to get a total distance. Since this is a String, the first approach that we will look at is to extract all the numbers out of the string and then sum them up. To do this, I created a function that accepts the String and then uses a combination of REGEXP, INSTR, and SUBSTR functions to extract the numbers out, which I then sum up.
Step 1: Create the function
I am attaching the function definition that you can compile in the database and use in your query.
Step 2: Add it to the SQL
I invoke the function and pass the 'distance' string as the only parameter
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,sum_distances(ltrim(sys_connect_by_path(distance, '+'), '+')) distance
from distances
where level = 7
and connect_by_root origin = destination
connect by nocycle origin = prior destination;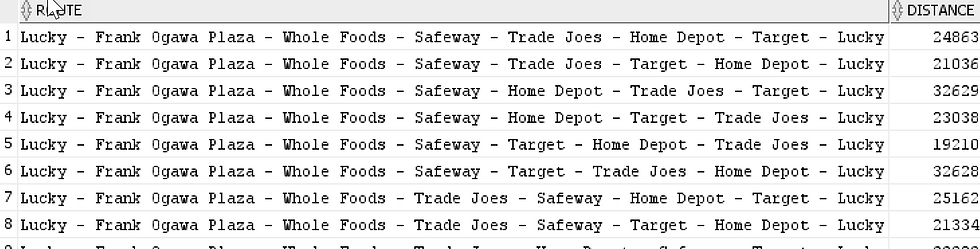
STAGE 4: Final-ish stage!
Now all you need to do is to order the output in ascending order of distances. The first row gives you the shortest path!
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,sum_distances(ltrim(sys_connect_by_path(distance, '+'), '+')) distance
from distances
where level = 7
and connect_by_root origin = destination
connect by nocycle origin = prior destination
order by distance;
In this case, you will get 7 rows with the same result. They are the same path, with each path starting at a different address. If you have a requirement to start from a "home" address, you can specify that into your query. In this example, I am setting Frank Ogawa Plaza, the address in Downtown Oakland, as my home address.
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,sum_distances(ltrim(sys_connect_by_path(distance, '+'), '+')) distance
from distances
where level = 7
and connect_by_root origin = destination
start with origin_name = 'Frank Ogawa Plaza'
connect by nocycle origin = prior destination
order by distance;
STAGE 5: The improved hack!
While the string manipulation does the trick for summing up the distances, I came across a much more elegant solution that could be applied here. This article details a solution around performing arithmetic operations in conjunction with hierarchical queries and coincidentally is very similar to what I worked on so far. However, instead of using string functions, I could just directly issue the string into an EXECUTE IMMEDIATE to get the result! Excellent!
Here's the modified function. Much fewer lines. Much less complexity.
STAGE 6: Goodbye stored procedure!
In our solution so far, we have a SQL query and a PL/SQL function. First, we need to have the function compiled in the database. Only then can the SQL be used. What if you do not wish to have this kind of dependency? We can get rid of the process of compiling a function in the DB and instead define it directly in the SQL and then use it in the query using the WITH clause.
I have named the function sum_dist to differentiate it from the previous function that we had created.
with
function sum_dist (p_distances in varchar2)
return number
as
ln_distance number := 0;
begin
execute immediate 'select '||p_distances||' from dual '
into ln_distance;
return ln_distance;
end sum_dist;
select ltrim(sys_connect_by_path(origin_name, ' - '), ' - ')||' - '||destination_name route
,sum_dist(ltrim(sys_connect_by_path(distance, '+'), '+')) distance
from distances
where level = 7
and connect_by_root origin = destination
start with origin_name = 'Frank Ogawa Plaza'
connect by nocycle origin = prior destination
order by distance;STAGE 7: The end?
In terms of getting a result, sure. However, I believe there is scope to improve the solution further primarily in two ways:
usage of more Oracle DB features. At the moment, I have used just the Hierarchical Query and the WITH clause features in this SQL. I have not even explored options like Optimizer Hints or used the scores of functions and features that come standard with SQL. One way to further improve on this solution would be to explore other features within Oracle DB that could get us the result faster.
exploring existing algorithms for solving TSP. When I started working on this (I was faced with a real-life requirement where I needed this problem solved every day - no, I was not hunting for toilet papers, I solved that problem in another way), I was not even aware of the term Traveling Salesman Problem, let alone the fact that is a well-known challenge in the world of computing. I came across TSP after I built this query and was helping a friend solve a similar problem. Another direction to take this would be to look at the existing algorithms that are available for solving TSP and look at efficient ways to implement them using SQL or PL/SQL.
I would be very interested to know if you have thoughts or ideas on tackling this more efficiently in Oracle DB.
I have applied this solution to build an application called Route Builder that can be accessed at https://routebuilder.app
For closing, here's the final path for our toilet paper run!

Comments